- PROJECTIFS (ESPACE ET REPÈRE)
- PROJECTIFS (ESPACE ET REPÈRE)PROJECTIFS ESPACE & REPÈREEspace projectif . Étant donné un espace vectoriel E sur un corps commutatif K, on considère dans E = E —0 la relation entre deux éléments x et y définie par:
La relation est une relation d’équivalence et l’ensemble quotient E / est appelé espace projectif déduit de E et est noté P(E). L’ensemble E est appelé espace vectoriel sous-jacent de P(E). Une classe d’équivalence, élément de P(E), est appelée point projectif; on désigne par 神 l’application canonique qui à un élément de E associe sa classe dans P(E). Lorsque E = Kn +1, l’espace projectif déduit se note Pn (K). Si E est de dimension n + 1, la dimension de P(E) est, par définition, n . Il faut toutefois remarquer que P(E) n’est pas un espace vectoriel.L’espace projectif réel ou complexe Pn (R) ou Pn (C) est une variété compacte non orientable. L’expace affine réel ou complexe de dimension n se plonge de manière naturelle dans cet espace projectif; ce plongement correspond géométriquement à l’adjonction de «points à l’infini», réels ou imaginaires, à cet espace affine.Variété linéaire projective . Soit F un sous-espace vectoriel de E, l’image par 神 de F = F —0 est, par définition, une variété linéaire projective de P(E). On peut aisément montrer que l’intersection d’une famille quelconque de variétés linéaires projectives est une variété linéaire projective et que l’espace vectoriel sous-jacent de cette intersection est l’intersection des espaces vectoriels sous-jacents des variétés de la famille. Une variété projective déduite d’un hyperplan de E s’appelle un hyperplan projectif, et sa dimension (lorsque dim (E) = n + 1) est égale à n — 1; un espace projectif de dimension 1 (resp. 2) est appelé droite projective (resp. plan projectif). Soit X un sous-ensemble de P(E); on appelle variété linéaire engendrée par X l’intersection de toutes les variétéq linéaires contenant X. Soit k + 1 points de P(E); on dit qu’ils forment une partie projectivement libre si la dimension de la variété engendrée par eux est égale à k ; ils sont projectivement liés si la dimension de la variété est inférieure à k . On peut montrer que k + 1 points 神(xi ) de P(E) sont libres si et seulement si les k + 1 points xi sont libres dans E. Ainsi, bien que P(E) ne soit pas un espace vectoriel, la notion d’indépendance se conserve. Par suite, on a des énoncés de théorèmes sur les dimensions équivalents aux énoncés sur les dimensions des sous-espaces vectoriels, en particulier le théorème de la «base incomplète».Coordonnées homogènes; repère projectif . Soit B = (ei ), 1 諒 i 諒 n + 1, une base de l’espace vectoriel E de dimension n + 1. Tout élément x de E s’écrit: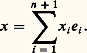
avec xi 捻 K. Le (n + 1)-uple (x 1, x 2, ..., xn +1) s’appelle système de coordonnées homogènes du point 神(x ) de P(E). Soit e 0 l’élément de E de coordonnées:
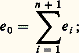On peut donner une représentation, à l’aide de coordonnées, d’une variété linéaire projective P(F): il suffit de donner la représentation du sous-espace vectoriel sous-jacent F privé de 0. Soit 神(gj ), 1 諒 j 諒 k + 1, une famille libre engendrant P(F). Désignons par (aij ), 1 諒 i 諒 n + 1, le système de coordonnées homogènes du point 神(gi ). Alors un système de coordonnées homogènes d’un point de P(F) est donné par:
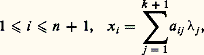où lesj appartiennent à K et ne sont pas tous nuls. Ces n + 2 formules définissent une bijection entre Pk +1(E) et P(F) qui est une représentation paramétrique de la variété projective.Dans le cas particulier de Pn (R), où Rn +1 est muni de la base canonique, le plongement, indiqué ci-dessus, de l’espace affine de dimension n identifié à Rn dans Pn (R) fait correspondre au point (1,2, ...n ) le point de coordonnées homogènes (1,2, ...,n ,n +1); les «points à l’infini» de Pn (R) sont caractérisés par la conditionn +1 = 0 et forment donc un hyperplan projectif.La géométrie projective est l’étude des espaces projectifs et des variétés linéaires projectives, ainsi que des invariants par le groupe projectif.
Encyclopédie Universelle. 2012.
